fitBsplineObjectToScatteredData

Fit a b-spline object to scattered data. This is basically a wrapper for the ITK filter https://itk.org/Doxygen/html/classitk_1_1BSplineScatteredDataPointSetToImageFilter.html. This filter is flexible in the possible objects that can be approximated. Possibilities include:

• curve:1/2/3/4-D

• surface:2-D surface in 3-D space (not available/templated)

• scalar:2/3/4-D scalar field

• displacement:2/3-D displacement field

• displacement:2/3-D time-varying velocity field

In order to understand the input parameters, it is important to understand the difference between the parametric and data dimensions. A curve as one parametric dimension but the data dimension can be 1-D, 2-D, 3-D, or 4-D. In contrast, a 3-D displacement field has a parametric and data dimension of 3. The scattered data is what's approximated by the B-spline object and the parametric point is the location of scattered data within the domain of the B-spline object.

fitBsplineObjectToScatteredData(
  scatteredData,
  parametricData,
  parametricDomainOrigin,
  parametricDomainSpacing,
  parametricDomainSize,
  isParametricDimensionClosed = NULL,
  dataWeights = NULL,
  numberOfFittingLevels = 4,
  meshSize = 1,
  splineOrder = 3
)

Arguments

scatteredData

matrix defining the scattered data input to be approximated. Data is organized by row –> data v, column —> data dimension.

parametricData

matrix defining the parametric location of the scattered data. Data is organized by row –> parametric point, column –> parametric dimension. Note that each row corresponds to the same row in the scatteredData.

parametricDomainOrigin

vector defining the parametric origin of the B-spline object.

parametricDomainSpacing

vector defining the parametric spacing of the B-spline object. Defines the sampling rate in the parametric domain.

parametricDomainSize

vector defining the size (length) of the B-spline object. Note that the length of the B-spline object in dimension d is defined as parametricDomainSpacing[d] * (parametricDomainSize[d]-1).

isParametricDimensionClosed

vector of bools defining whether or not the corresponding parametric dimension is closed (e.g., closed loop). Default = FALSE.

dataWeights

vector defining the individual weighting of the corresponding scattered data value. Default = NULL meaning all values are weighted the same.

numberOfFittingLevels

integer specifying the number of fitting levels.

meshSize

vector defining the mesh size at the initial fitting level.

splineOrder

spline order of the B-spline object. Default = 3.

Value

Matrix for B-spline curve. Otherwise, returns ANTsR image.

Author

NJ Tustison

Examples

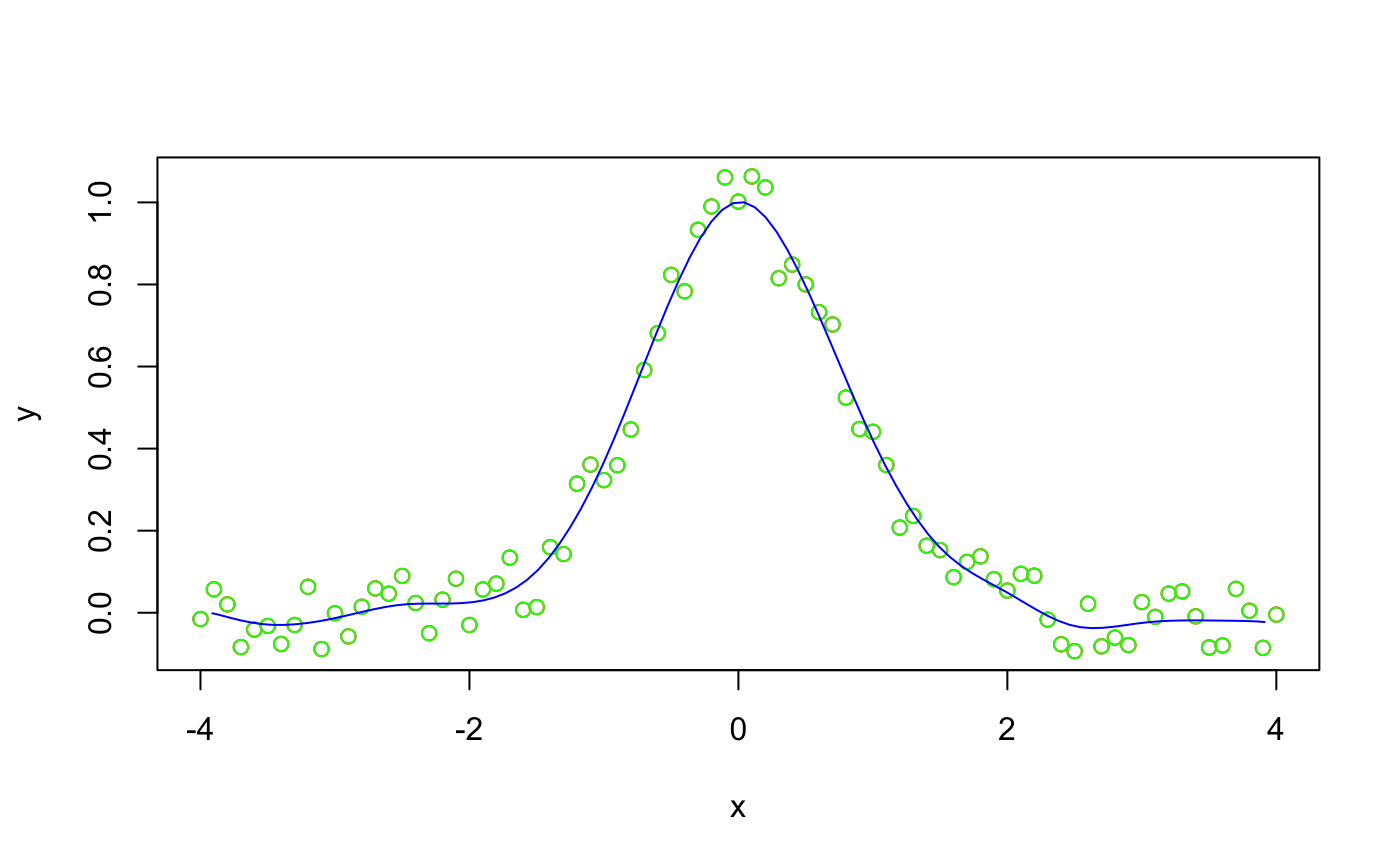
# Perform 2-D curve example

x <- seq(from = -4, to = 4, by = 0.1)
y <- exp(-(x * x)) + runif(length(x), min = -0.1, max = 0.1)
u <- seq(from = 0.0, to = 1.0, length.out = length(x))
scatteredData <- cbind(x, y)
parametricData <- as.matrix(u, ncol = 1)
numberOfSamplePoints <- 100
spacing <- 1 / (numberOfSamplePoints - 1) * 1.0
bsplineCurve <- fitBsplineObjectToScatteredData(scatteredData, parametricData,
  parametricDomainOrigin = c(0.0), parametricDomainSpacing = c(spacing),
  parametricDomainSize = c(numberOfSamplePoints), isParametricDimensionClosed = c(FALSE),
  numberOfFittingLevels = 5, meshSize = 1
)

plot(x, y, "p", col = "red")
points(scatteredData[, 1], scatteredData[, 2], col = "green")
lines(bsplineCurve[, 1], bsplineCurve[, 2], col = "blue")


# Perform 2-D scalar field (i.e., image) example

numberOfRandomPoints <- 10000

img <- antsImageRead(getANTsRData("r16"))
imgArray <- as.array(img)
rowIndices <- sample(2:(dim(imgArray)[1] - 1), numberOfRandomPoints, replace = TRUE)
colIndices <- sample(2:(dim(imgArray)[2] - 1), numberOfRandomPoints, replace = TRUE)

scatteredData <- as.matrix(array(data = 0, dim = c(numberOfRandomPoints, 1)))
parametricData <- as.matrix(array(data = 0, dim = c(numberOfRandomPoints, 2)))
for (i in seq_len(numberOfRandomPoints))
{
  scatteredData[i, 1] <- imgArray[rowIndices[i], colIndices[i]]
  parametricData[i, 1] <- rowIndices[i]
  parametricData[i, 2] <- colIndices[i]
}

bsplineImage <- fitBsplineObjectToScatteredData(scatteredData, parametricData,
  parametricDomainOrigin = c(0.0, 0.0), parametricDomainSpacing = c(1.0, 1.0),
  parametricDomainSize = dim(img),
  numberOfFittingLevels = 7, meshSize = c(1, 1)
)
plot(bsplineImage)